Antireflection Coatings for Two Zeros

In some applications, antireflection coatings are required to have zero reflectance at specific, well-defined wavelengths, rather than across a wide spectral range. A common example is frequency doubling, where the coating must eliminate reflections at two wavelengths, one being twice the other.

Quarter-Quarter Coating

The simplest design for this requirement is the quarter-quarter coating, as previously discussed. This coating achieves two reflectance zeros at:

\[
\lambda = \frac{3\lambda_0}{4} \quad \text{and} \quad \lambda = \frac{3\lambda_0}{2}
\]

The conditions for this design are:

\[
n_1 = \sqrt{\frac{n_0 n_m}{n_2}}, \quad n_2 = \sqrt{\frac{n_0 n_m}{n_1}}
\]

where \(n_0\) is the refractive index of air, \(n_1\) and \(n_2\) are the indices of the coating layers, and \(n_m\) is the substrate index.

Limitations for Low-Index Substrates

The lowest achievable coating index, typically 1.38 (e.g., magnesium fluoride), restricts the substrate index to a minimum of:

\[
n_m = 1.38^3 = 2.63
\]

This makes the design unsuitable for low-index substrates.

Example: Lithium Niobate

Lithium niobate \((n_m \approx 2.25)\) often requires coatings at wavelengths \(\lambda\) and \(2\lambda\).
For this material, the ideal indices would be:

\[
n_1 = 1.310, \quad n_2 = 1.717
\]

Using \(n_1 = 1.38\) and \(n_2 = 1.717\), the reflectance is reduced to 0.2%, which is acceptable for many applications. Adjusting \(n_2\) between 1.7 and 1.8 yields similar performance.

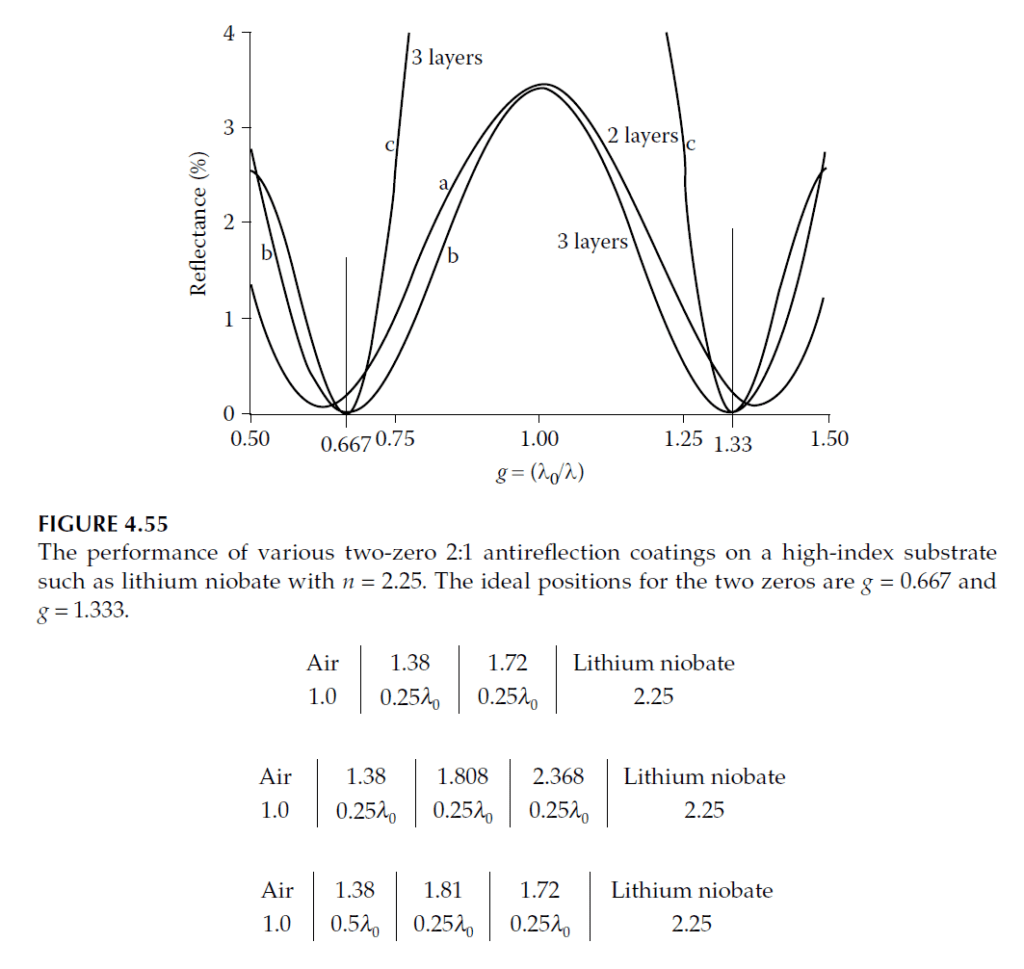
Adding an Additional Layer

For applications requiring even lower reflectance, a third layer can be introduced. By keeping all layers as quarter-waves or multiples thereof, the design retains symmetry about \(g = 1\).

Designing the Third Layer

The quarter-quarter design can be enhanced by adding a high-index layer \((n_3 > n_m)\).
The additional layer modifies the vector diagram, trimming the amplitude reflection coefficient \((\rho_a)\) to achieve equal-length vectors forming an equilateral triangle.

Example Design:

\[
\text{Air → Layer 1: } n_1 = 1.38, \quad \text{Layer 2: } n_2 = 1.808, \quad \text{Layer 3: } n_3 = 2.368, \quad \text{Substrate: } n_m = 2.25
\]

Performance

Using zinc sulfide \((n_3 = 2.35)\) for the third layer and \(n_2\) values between 1.75 and 1.85, the reflectance at \(g = 2/3\) can be reduced to below 0.1%.

Alternative Half-Wave Design

Instead of a quarter-wave for the first layer, a half-wave layer can be used. This combines with the next layer’s reflection coefficient \((\rho_c)\) for enhanced performance.

Example Design:

\[
\text{Air → Layer 1 (Half-Wave): } n_1 = 1.38, \quad \text{Layer 2 (Quarter-Wave): } n_2 = 1.81, \quad \text{Layer 3 (Quarter-Wave): } n_3 = 1.72, \quad \text{Substrate: } n_m = 2.25
\]

This design is flexible, allowing \(n_2\) and \(n_3\) adjustments to achieve reflectance below 0.1%.

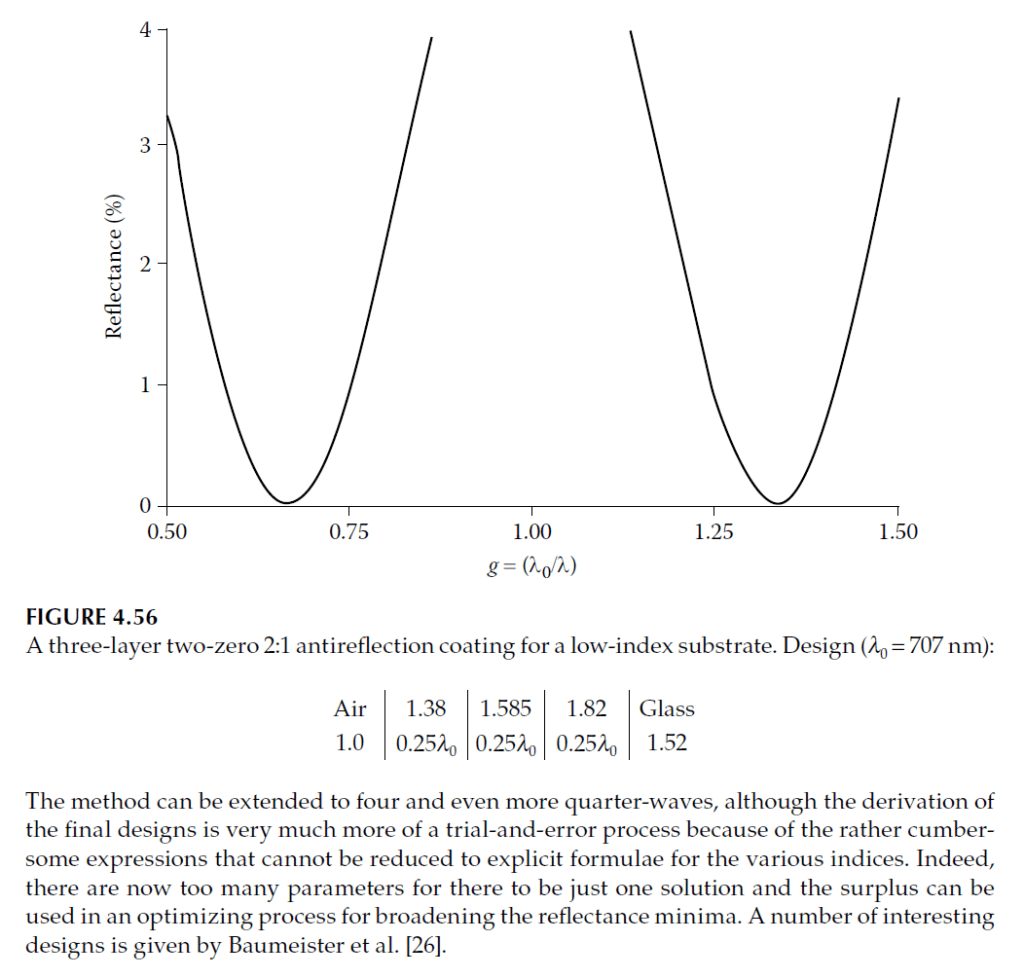
Quarter-Quarter-Quarter Design for Low-Index Substrates

For substrates with lower indices, a three-layer quarter-wave design is effective. An example configuration:

\[
\text{Air → Layer 1: } n_1 = 1.38, \quad \text{Layer 2: } n_2 = 1.808, \quad \text{Layer 3: } n_3 = 2.368, \quad \text{Substrate: } n_m = 1.52
\]

Performance

With monitoring at 707 nm, this design achieves reflectance zeros at 530 nm and 1.06 μm (Figure 4.56).

Mouchart’s Technique

Mouchart proposed a systematic method for designing coatings with zeros at two specific wavelengths. The approach involves:

Predefining all layer thicknesses as multiples of quarter-waves.
Arbitrarily selecting indices for all but the final two layers.
Solving an eighth-order equation to calculate the indices of the remaining layers.

The calculation can also utilize the second derivative of reflectance \((\partial^2R/\partial\lambda^2)\) at the antireflection wavelength to select the best designs from numerous possibilities.

Example

Mouchart explored three-layer coatings in detail, providing an analytical foundation for these specialized designs.

This tutorial highlights the flexibility of antireflection coatings tailored for applications requiring two reflectance zeros, offering various designs from simple quarter-quarter arrangements to more complex multi-layered systems.

Request a Quote

Antireflection Coatings for Two Zeros