Introduction

In the field of optical thin film design, the question arises: can we automate the process of refining and optimizing a design to achieve its best possible performance? The answer is a conditional yes. Automation in thin film design typically takes two forms:

• Refinement: Improving an existing design by making minor adjustments.
• Synthesis: Constructing a design from scratch or significantly altering an existing one.

Together, these processes are referred to as optimization, although the definitions of these terms are not universally agreed upon. Optimization, whether by refinement or synthesis, is guided by the figure of merit — a numerical value representing how closely a design meets its desired performance.

Defining the Figure of Merit

1. Calculation of Merit:

– The figure of merit (F) quantifies the difference between the actual and desired performance of a coating. A typical formula is: \[F = \frac{\sum W_j \left| T_j – P_j \right|^q}{\sum W_j},\] where:

• \(T_j\): Target performance at the \(j\)th point.
• \(P_j\): Calculated performance at the same point.
• \(W_j\): Weight assigned to each target point.
• \(q\): Power to which the performance gap is raised, often set to \(q = 2\).

2. Importance of Continuity:

• The function of merit must vary continuously with the design parameters to ensure efficient and reliable optimization. Abrupt changes or hard constraints can hinder this process.

3. Optimization Objective:

• When the number of design parameters matches the number of targets, the optimization problem may have a complete solution, provided the targets are achievable. However, in most cases, there are fewer parameters, requiring the optimization process to minimize the figure of merit as much as possible.

Finding the Global Minimum

1. Multidimensional Space:

• The figure of merit can be visualized as a surface in a multidimensional space, with dimensions corresponding to design parameters and the figure of merit. The **global minimum** represents the lowest value of merit.

2. Challenges in Finding the Minimum:

– For complex designs, an exhaustive search of all possible parameter combinations is computationally infeasible. For example:

• A 20-layer design, each layer having 20 possible thickness values, results in \(20^{20}\) combinations. At 1 nanosecond per calculation, this would take 2 billion years to complete.

3. Optimization Techniques:

• Instead of exhaustive searches, limited procedures are used to find local minima or approximate global minima. Some techniques search across parameter space to improve the chances of finding the constrained global minimum.

Refinement Techniques

1. Starting Design:

• Refinement begins with an initial design that may already perform adequately. The process adjusts parameters such as layer thicknesses or refractive indices to achieve the **nearest local minimum** of the merit function.

2. Steepest Descent Method:

• This method follows the steepest slope of the merit function but may result in zigzag convergence. The step size is adjusted to prevent instability.

3. Damped Least Squares:

• This approach minimizes the sum of squared deviations between actual and target performance values, providing stable and efficient convergence.

4. Univariate and Linear Search Methods:

• Univariate Search: Adjusts one parameter at a time using techniques like the golden section method for efficient bracketing of minima.
• Linear Search: Freely chooses search directions in parameter space, often using conjugate directions for efficiency.

5. Flip-Flop Optimization:

• Layers are represented by two possible indices (high and low). The figure of merit is recalculated iteratively for each layer, switching indices to minimize merit.

Synthesis Techniques

1. Constructing a Design:

• Synthesis involves adding layers to an initial design, refining the resulting structure at each step. The process continues until no further improvement is possible.

2. Needle Variation Method:

• A thin slice of material (needle) is added to the design where it reduces the merit function most effectively. This approach is particularly useful for designs requiring high precision.

3. Statistical Techniques:

• Methods like simulated annealing and statistical testing explore parameter space by introducing randomness, which helps avoid local minima and increases the chances of finding the global minimum.

4. Challenges of Synthesis:

• Synthesis can lead to designs with thin layers that are difficult to manufacture, requiring post-processing to simplify the structure.

High-Reflectance Coatings

1. Fringe Effects (Figure 16.20):

• High-reflectance coatings are prone to narrow fringes caused by multiple-beam interference. These fringes may align between target points, creating performance gaps not addressed by the merit function.

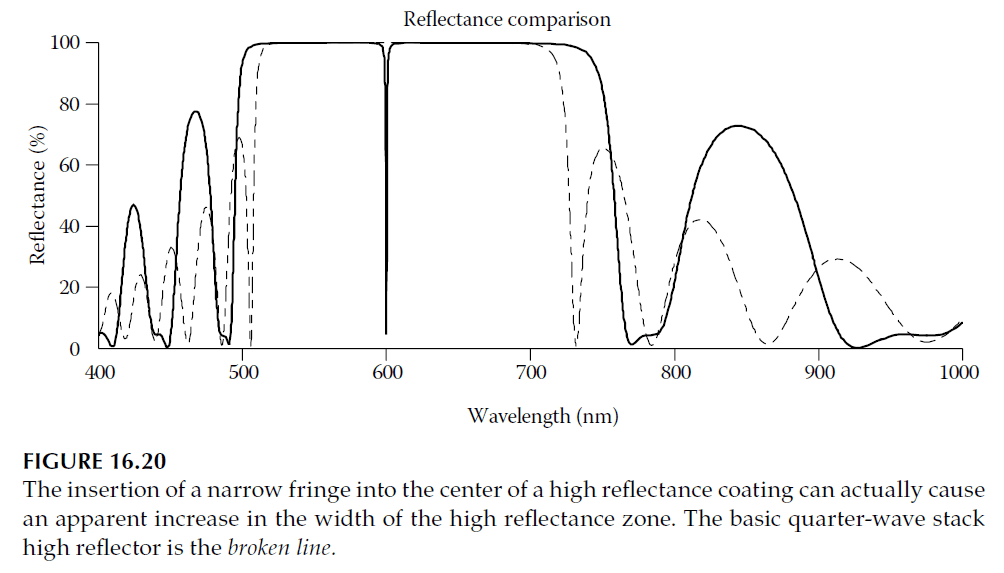
2. Target Density Requirements:

• To avoid aliasing, the number of target points should increase with coating thickness. For a coating with \(m\) quarter-waves at a wavelength \(\lambda\), the target density should be: \[\frac{\lambda}{m}.\]

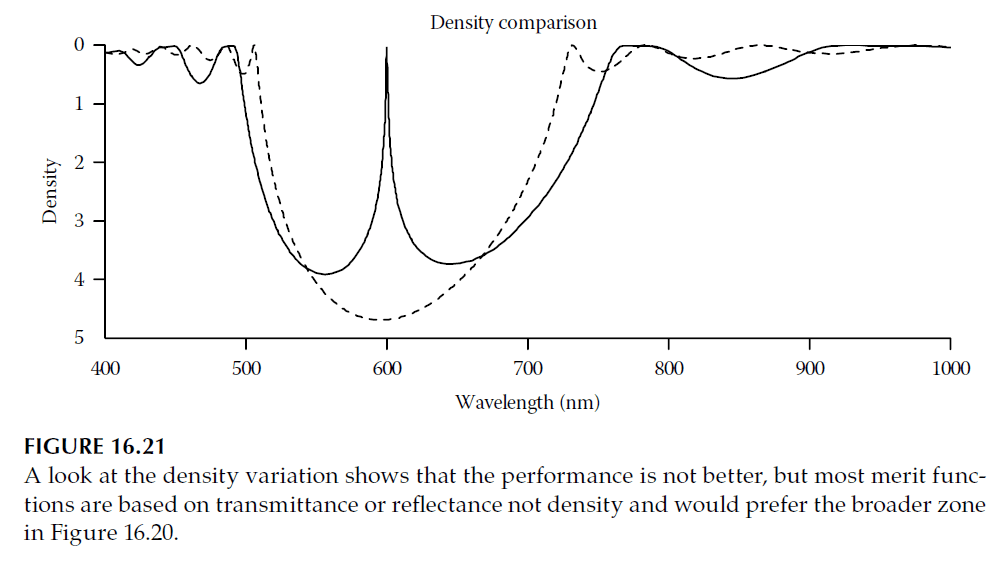
3. Fringe Persistence:

• Figure 16.21 illustrates how narrow fringes persist in high-reflectance coatings, even after optimization. These features require specialized techniques for elimination.

Computational Considerations

1. Increased Complexity:

• As coating designs grow more complex (e.g., polymeric films with thousands of layers), computational demands increase exponentially. Automatic methods must balance precision with practicality.

2. Limits of Automation:

• While automatic methods have revolutionized coating design, they cannot replace the skill, experience, and innovation of designers. Further advancements in merit functions and optimization techniques are necessary for future progress.

Conclusion

Automatic methods in thin film design have transformed the field, enabling the refinement and synthesis of increasingly complex coatings. However, they remain limited by computational constraints and the inherent complexity of high-performance designs. The continued interplay of human expertise and computational power is essential for advancing optical coating technology.