Introduction
The rise of ultrafast laser systems, capable of generating light pulses as short as a few femtoseconds (fs), has introduced a critical need for coatings that can handle transient optical effects.
Traditionally, optical coatings have been designed under steady-state assumptions, where time-dependent effects were negligible. However, with pulses as short as 5 fs, the interaction time with coatings is on the same order as the pulse duration, making transient effects significant.
These challenges are compounded by group velocity dispersion (GVD) and higher-order dispersion effects, which alter the pulse shape and carrier-envelope phase. The need for coatings that not only reflect or transmit light but also control phase and dispersion is paramount, leading to innovations such as chirped mirrors and Gires-Tournois interferometers (GTI).
The Nature of Ultrafast Pulses
1. Pulse Travel and Interaction Time:
- A typical high reflector, such as a quarter-wave stack, consists of 25 alternating layers of high and low refractive indices. For a wavelength of 1 µm, the light’s round-trip path through such a coating is approximately 12.5 µm, corresponding to a travel time of 42 fs.
- – Pulses shorter than this interaction time demand precise transient-response modeling.
2. Pulse Representation:
– An ultrafast pulse can be described using two equivalent models:
- As an envelope superimposed on a carrier wave. The envelope represents the energy distribution, while the carrier determines the phase properties.
- As a superposition of monochromatic waves with a continuous frequency distribution. These waves interfere coherently to form the pulse.
3. Gaussian Pulse Envelope:
- A Gaussian pulse envelope is commonly used to describe ultrafast pulses. At \(z = 0\), it is given by: \[
F(t) = A e^{-t^2 / 2\mu^2}, \] where \(\mu\) determines the pulse’s temporal spread. - The Fourier transform of this envelope yields a frequency-domain Gaussian: \[G(\omega) = B e^{-(\omega – \omega_0)^2 / 2\mu^2}.\]
4. Pulse Width and Spectral Width Relationship:
- The pulse duration (\(\tau\)) and spectral width (\(\Delta \omega\)) are inversely related: \[\tau \cdot \Delta \omega = 4 \ln 2.\] This highlights the trade-off between temporal and spectral resolution for ultrafast pulses.
5. Phase and Group Velocities:
- The pulse consists of an envelope (traveling at the group velocity, \(v_g\)) and a carrier wave (traveling at the phase velocity, \(v_p\)). Dispersion causes \(v_g\) and \(v_p\) to differ, resulting in the carrier wave “slipping” through the envelope.
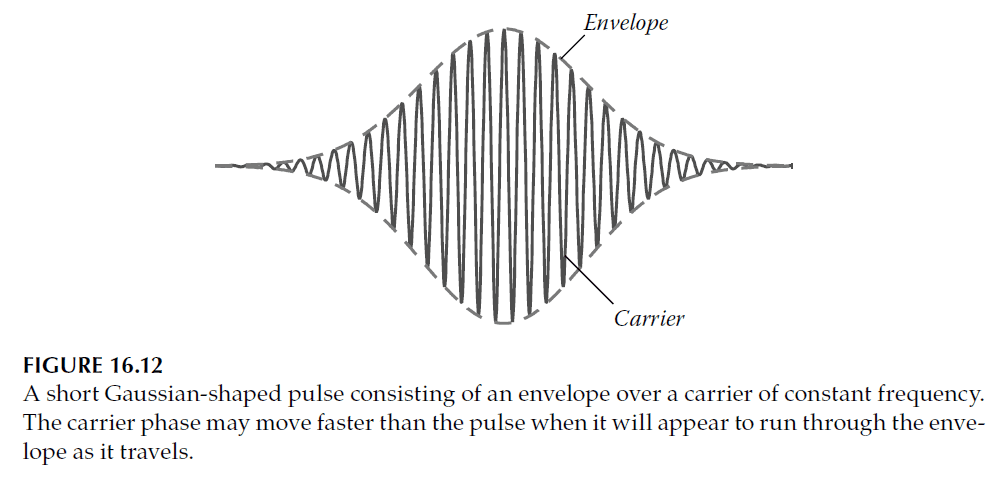
6. Pulse Visualization (Figure 16.12):
- Figure 16.12 shows a Gaussian pulse envelope with a carrier wave. The distinction between group velocity and phase velocity is evident in how the carrier oscillates within the envelope.
Dispersion and Its Effects
1. Group Velocity Dispersion (GVD):
- GVD quantifies how the group velocity varies with frequency. It is defined as: \[\text{GVD} = \frac{d^2\kappa}{d\omega^2},\] where \(\kappa = 2\pi n/\lambda\) is the wave vector.
2. Pulse Broadening Due to GVD:
- In dispersive media, different spectral components of the pulse travel at different speeds, causing the pulse to broaden. For a Gaussian pulse, the broadened pulse width after traveling a distance \(z\) is: \[\tau_{\text{new}} = \tau \sqrt{1 + \left(\frac{4 \ln 2 \cdot \text{GVD} \cdot z}{\tau^2}\right)}.\] This relationship shows that shorter pulses, with their broader spectra, are more susceptible to broadening.
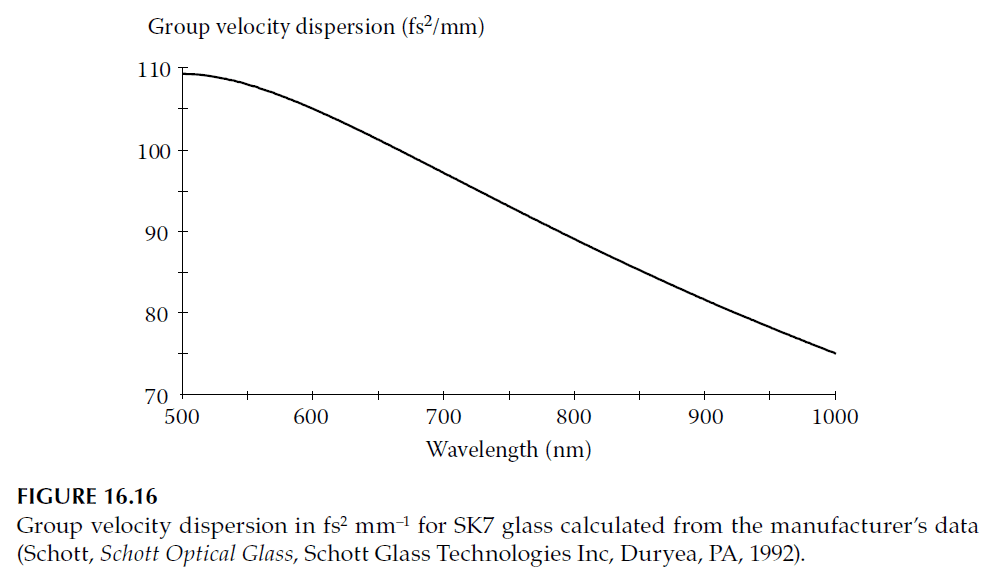
3. Group Velocity Dispersion in Optical Materials (Figure 16.16):
- Figure 16.16 illustrates GVD data for SK7 glass, showing how pulse broadening occurs even over millimeter-scale propagation distances.
4. Higher-Order Dispersion:
- Beyond GVD, higher-order effects like third-order dispersion (TOD) also influence pulse dynamics. TOD becomes significant in broadband systems and is quantified as the third derivative of \(\kappa\) with respect to \(\omega\).
5. Group Delay and Group Delay Dispersion (Equations 16.13 and 16.14):
- The group delay (GD) measures the time delay introduced by a coating: \[\text{GD} = -\frac{d\phi}{d\omega}.\]
- The group delay dispersion (GDD) measures how GD varies with frequency: \[\text{GDD} = -\frac{d^2\phi}{d\omega^2}.\]
- Equation 16.14 relates the broadened pulse width (\(\tau_{\text{new}}\)) to the group delay dispersion.
Optical Coatings for Ultrafast Applications
1. Amplitude and Phase Modulation:
- Optical coatings affect both the amplitude and phase of light, enabling control over ultrafast pulses. The coating’s dispersion properties directly impact pulse broadening and chirping.
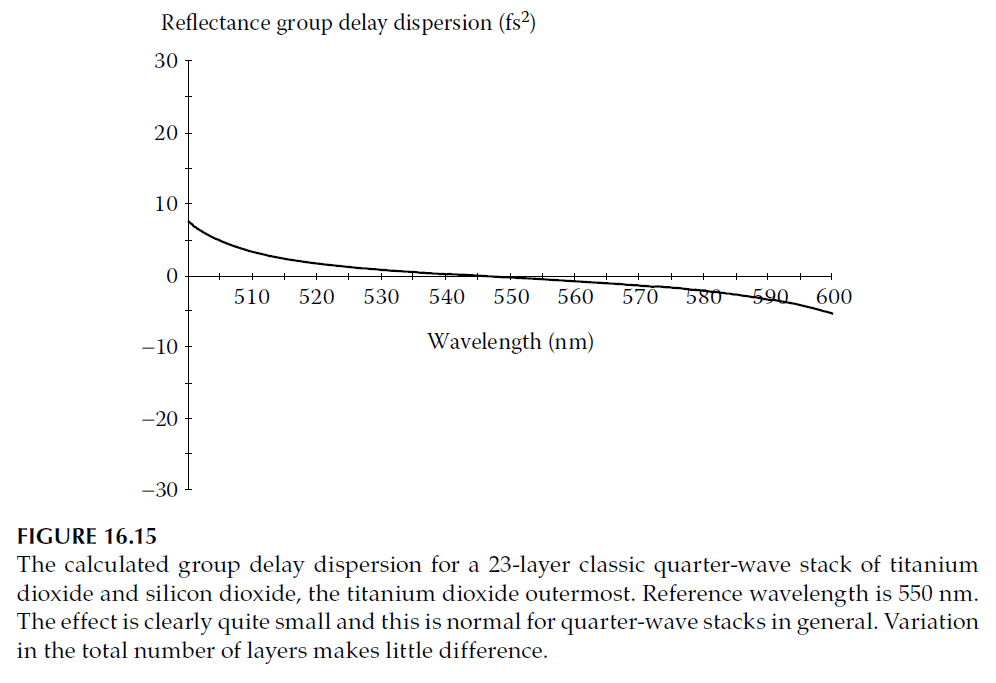
2. Quarter-Wave Stacks (Figure 16.15):
- Quarter-wave stacks are widely used in traditional applications due to their simplicity and minimal GDD. Figure 16.15 shows the calculated GDD for a quarter-wave stack with a high-index outermost layer.
Advanced Coating Designs
1. Chirped Mirrors:
– Chirped mirrors consist of layers with gradually varying thicknesses, allowing for precise phase adjustments over a broad spectral range. They are ideal for correcting chirped pulses.
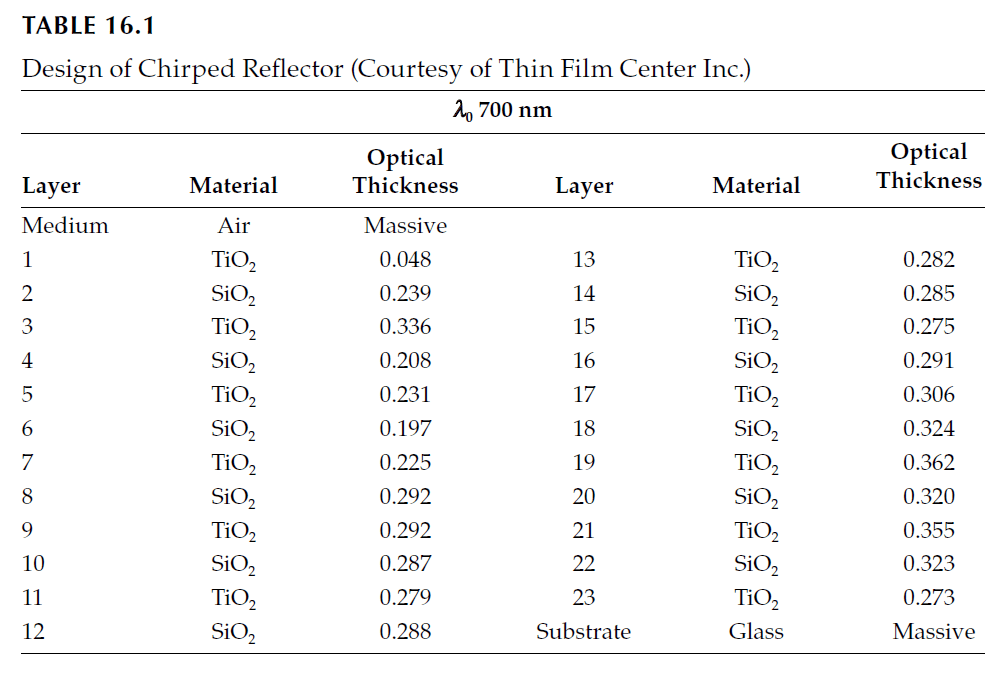
– Design Example:
- A chirped mirror designed for a GDD of \(-30^\circ\) over the 750–900 nm spectral range is detailed in Table 16.1, Figure 16.17, and Figure 16.18.
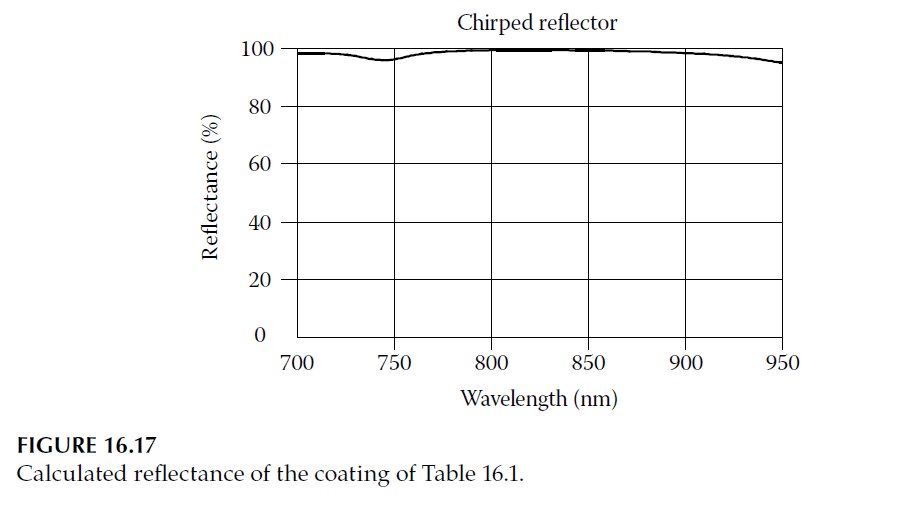
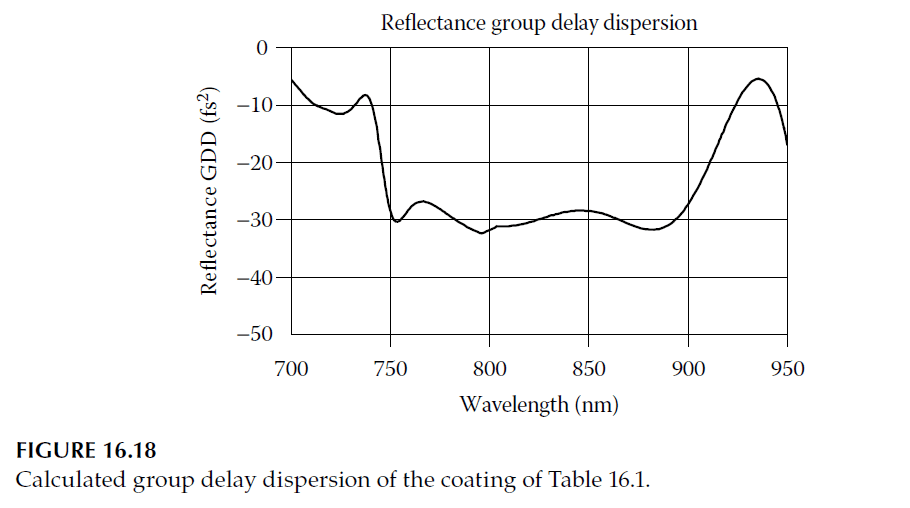
2. Gires-Tournois Interferometers (GTI):
– GTIs incorporate a weak optical cavity in front of a quarter-wave stack. This cavity introduces sharp phase variations, enhancing GDD in a narrow spectral range.
– Design Example:
- A GTI with the structure: \[\text{Air | (HL) HH(LH) L(HL) H | Glass}.\]
- The dispersive parameters of this design are shown in Figure 16.19.
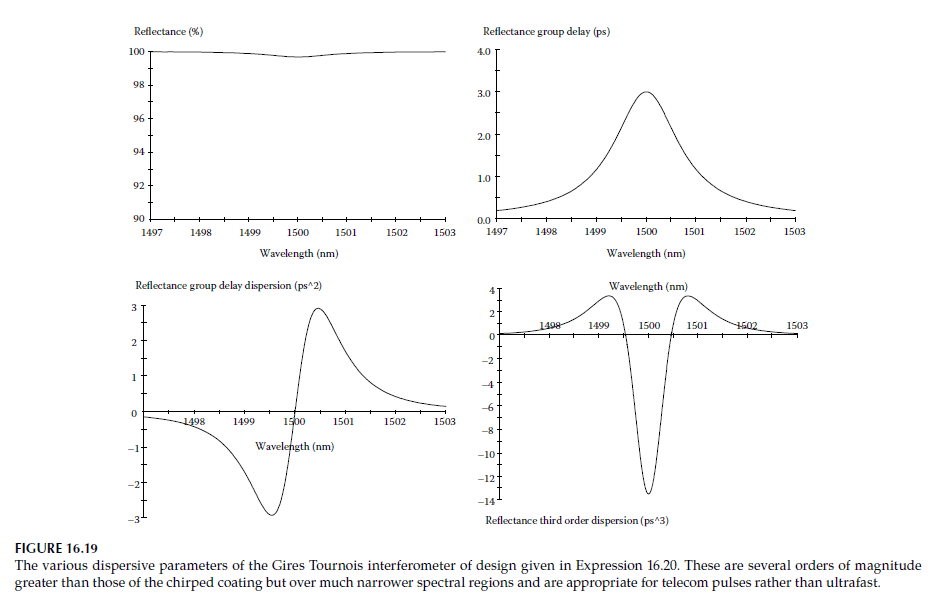
3. Metal-Enhanced GTIs:
- Metal layers, such as silver, can replace sections of GTIs to reduce the total number of layers while maintaining performance. Proper design ensures that reflectance is not compromised.
Practical Applications and Limitations
1. Telecommunications:
- In optical fiber systems, even picosecond pulses experience significant dispersion over kilometer-scale distances. Coatings with high GDD are essential for maintaining signal fidelity.
2. Material Dispersion:
- Normal dispersion in materials like glass can degrade ultrafast pulses over millimeter-scale distances. Coatings are crucial to compensating for these effects.
3. Chirped Mirrors vs. GTIs:
- Chirped mirrors provide broadband dispersion control, while GTIs are more effective in narrowband applications requiring high GDD.
Conclusion
The development of ultrafast coatings has pushed the boundaries of optical technology, addressing the challenges of transient effects in ultrafast lasers.
Advanced designs, such as chirped mirrors and Gires-Tournois interferometers, offer precise control over dispersion and phase, enabling their use in laser pulse shaping, telecommunications, and high-speed optical systems.
